Soluciones a la cuadrícula de 4×4: un enigma geométrico
La semana pasada se presentó una solución para unir una cuadrícula de 4×4 puntos utilizando solo seis trazos rectilíneos. Este es un desafío interesante que invita a un análisis más profundo de la geometría. A continuación, se muestra una alternativa que produce un resultado elegantemente simétrico y cíclico.
Cuadrículas y sus soluciones
En el caso particular de la cuadrícula de 3×3, la solución es única. Sin embargo, para la cuadrícula de 4×4, se conocen al menos tres soluciones distintas, aunque es probable que existan muchas más. A medida que aumenta la cantidad de puntos en la cuadrícula, también lo hace la posibilidad de encontrar diferentes soluciones.
El diseño de tapas de alcantarillas
Las tapas de alcantarillas presentan varias ventajas al ser redondas. Un motivo clave es que su forma circular permite trasladarlas rodando, facilitando su movimiento a pesar de su peso considerable. Además, estas tapas se ajustan en su hueco en cualquier orientación, a diferencia de las formas cuadradas, que requieren ser alineadas de manera precisa. Otra razón importante es que las tapas redondas no pueden caer a través de su propio hueco, lo que sería factible si tuvieran una forma cuadrada, ya que la diagonal de un cuadrado es más larga que su lado.
Esto plantea una interesante pregunta: ¿existe alguna otra forma para una tapa de alcantarilla que impida que se caiga por su propio hueco, o es la forma circular la única con esta propiedad?
La curvatura de las hojas de sable
Un aspecto fascinante sobre las hojas de sable es que sus formas son arcos de circunferencia, especialmente en aquellos sables que tienen vaina, como las katanas. Esto se debe a que la recta y la circunferencia son las únicas líneas que pueden deslizarse sobre sí mismas. Si la curvatura de un sable no fuera un arco, no podría insertar la hoja en la vaina de manera efectiva.
La resistencia de los triángulos en la construcción
Los triángulos son fundamentales en diversas estructuras debido a que son el único polígono cuya forma está determinada por la longitud de sus lados. Por ejemplo, un cuadrilátero con lados de 10 cm podría ser un cuadrado o un rombo, mientras que un triángulo con lados de 10, 20 y 30 cm es siempre un triángulo rectángulo. Esta característica hace que un triángulo sea indeformable, a menos que se rompa, contrastando con las estructuras basadas en cuadrados que son más propensas a deformarse.
La prevalencia de cuadrados y rectángulos
La abundancia de formas cuadradas y rectangulares en la arquitectura y el diseño humano también responde a razones prácticas. La gravedad favorece el movimiento en un plano horizontal, por lo que los ángulos rectos proporcionan estabilidad. Además, los objetos ortoédricos, como cajas y ladrillos, se ensamblan de manera eficiente, maximizando el uso del espacio. Por ejemplo, en la construcción de estructuras compactas, los ladrillos y tatamis se benefician de una relación de dimensiones que facilita su apilamiento.
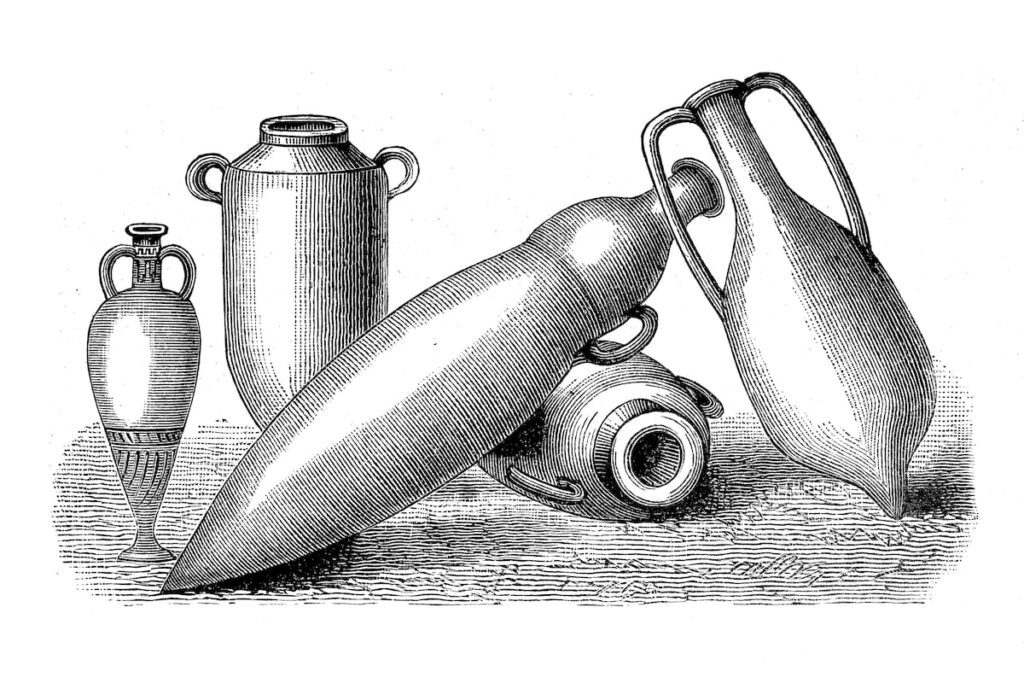
El diseño de ánforas romanas
A pesar de las ventajas de las formas rectangulares, las ánforas de los antiguos romanos eran puntiagudas y no podían sostenerse sobre su base. Este diseño tenía una relación superficie-volumen que resultaba poco ventajosa. La ingeniosidad de los romanos en la ingeniería y el diseño industrial se ve reflejada en este tipo de vasijas, que representan un equilibrio entre funcionalidad y estética.